Das Kaktovik Zahlensystem - was ist das denn?!
Das Kaktovik Zahlensystem ist ein ziemlich neues Rechensystem, was von einer Schule in einem kleinen Ort ganz im Norden von Alaska in den 90iger Jahren des letzten Jahrhunderts entwickelt worden ist. Hintergrund war, dass die Sprache der Inupiaq gar nicht zu unserem Zehnersystem, wie auch wir es in Europa benutzen, passte. Die Zahlbegriffe der Inupiaq sind auf einem Vigesimalsystem aufgebaut. Das bedeutet, die Basis des Stellenwertsystems hat nicht die Zehn, sondern die Zwanzig als Basis. Die Stellenwerte haben eine weitere Unterteilung in Fünferbündel. Dieses System ist durch das Abzählen von Fingern und Zehen entstanden. Die Finger und Zehen sind in Fünfergruppen (pro Hand und Fuß) gruppiert und insgesamt zwanzig.
Die Menschen, die sich dieses Zahlensystem ausgedacht haben, wollten die Zahldarstellung möglichst konsistent zu dieser Struktur bilden. Dadurch ist diese Schreibweise sehr gut in der Inupiaqsprache benutzbar und viele Rechnungen sind deutlich einfacher als in unserem Dezimalsystem durchzuführen.
Wie werden die Zahlen dargestellt?
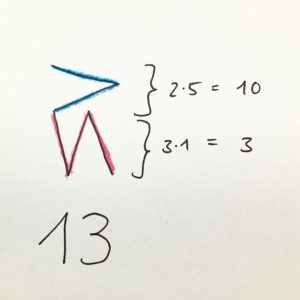

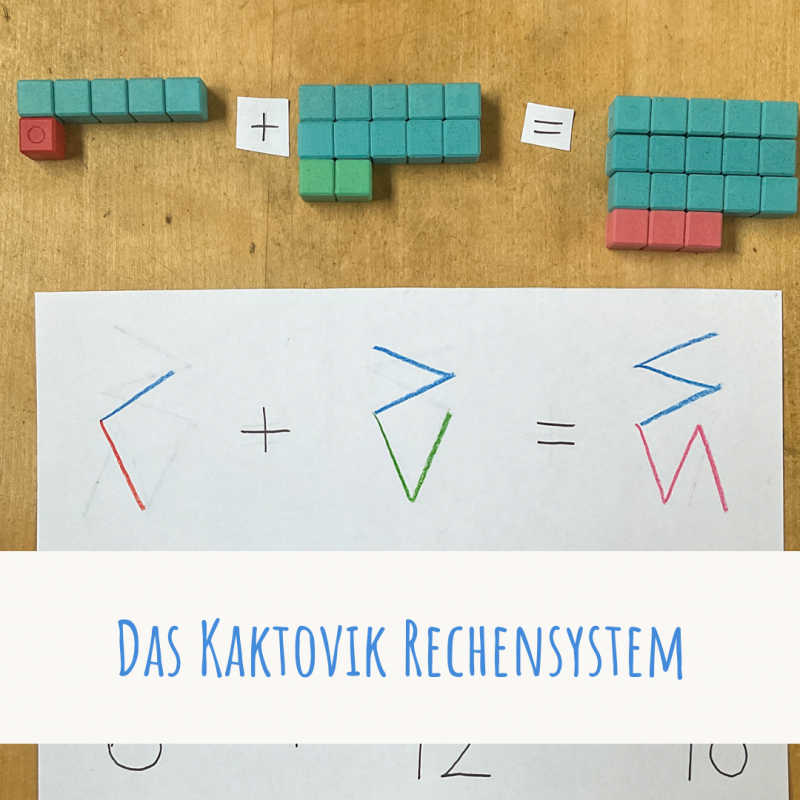
Die Erfinder des Systems wollten eine möglichst ikonische, abstrakte Darstellung, die die Struktur genau abbildet. Die Zahlen bestehen deswegen aus zwei Teilen: einem oberen und einem unteren Bereich. Im oberen Teil sind die Anzahl der Fünferbündel als Striche dargestellt, die schräg quer verlaufen. Im unteren Teil sind die Einer dargestellt als schräge senkrechte Striche. Auf der linken Abbildung siehst du die Zahl 13. In der 13 steckt zweimal die 5 und noch 3 Einer. In der rechten Abbildung siehst du die Zahlen von 0 bis 19. Bei 20 geht es dann mit einer weiteren Stelle weiter, die genauso wie in unserem Zahlensystem links daneben geschrieben wird.
Wie addiert man nun?
Ich zeige hier erstmal ein einfaches Beispiel der Addition, also wie man zusammenrechnet.
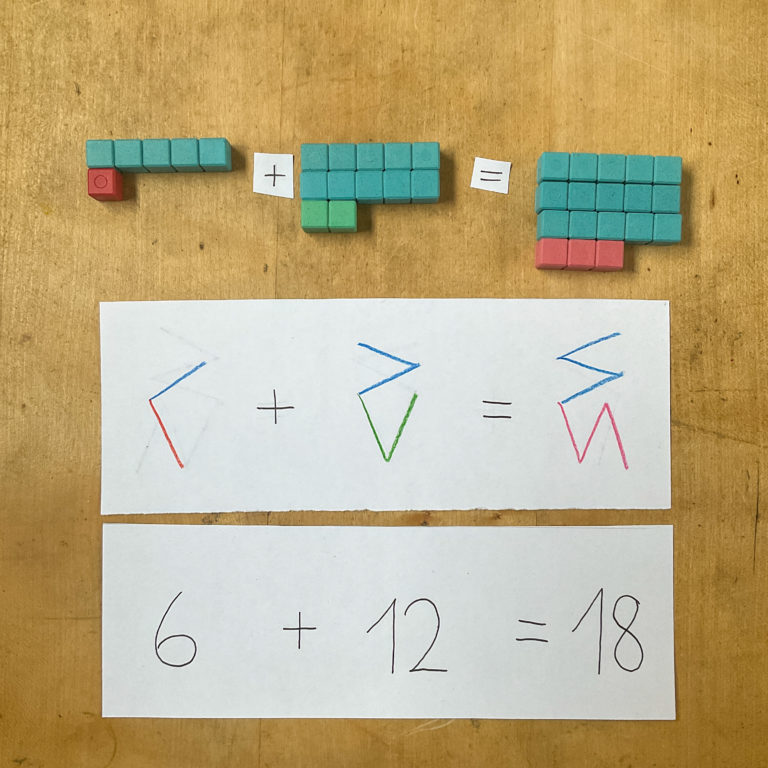
In dem Beispiel siehst du ganz schön, dass sich die Schreibweise der Katkovik direkt mit den Montessorirechenstäbchen übersetzen lässt. Jeder obere Querstrich entspricht einem Fünfer und jeder untere Strich einem Einer. Die oberen und unteren Teile der Zahl lassen sich so sehr komfortabel getrennt zusammenrechnen – erst die Einer, dann die Fünfer. Dies lässt sich auch bei den anderen Grundrechenarten vorteilhaft nutzen.
Addition mit Übertrag
Die wahre Power der Schreibweise wird klar, wenn man anfängt, mit Überträgen zu rechnen – da zeigen sich die Vorteile der konsistenten Zählweise mit Strichen. Ich habe zwei Aufgaben gelegt, wir fangen an mit einem Fünferübergang.
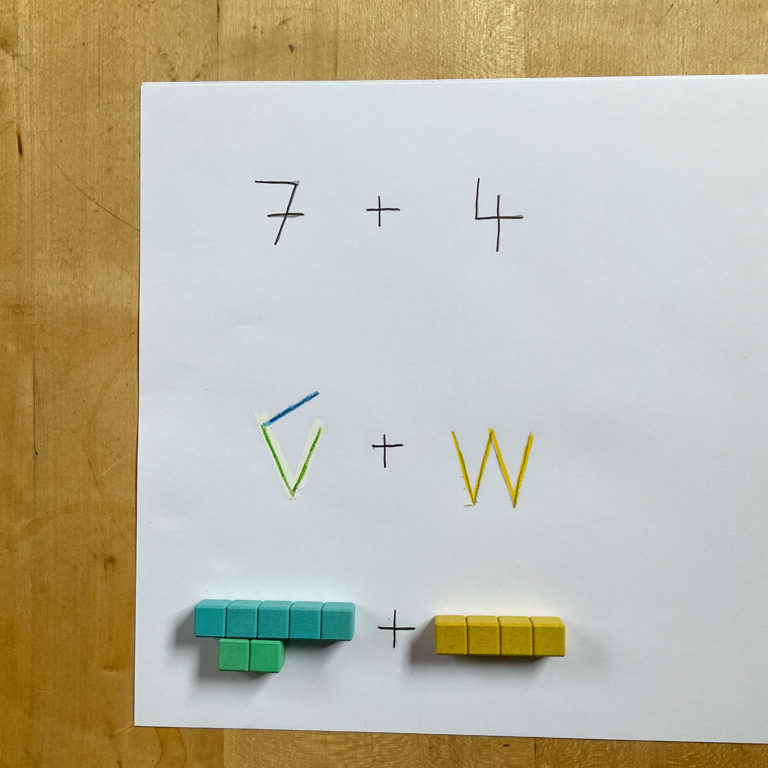
Die Zahl 7 wird im Kaktovik als 5 + 2 dargestellt, also einen schrägen Querstrich und zwei schäge senkrechte Striche. Die 4 sind einfach vier Einer, also vier senkrechte schräge Striche. Addieren bedeutet einfach zusammenkoppen, und das lässt sich auch in dieser Schreibweise gut darstellen – ich schreibe einfach alle Querstriche zusammen auf und alle senkrechten Striche. Um den Übertrag kümmere ich mich erst im nächsten Schritt.
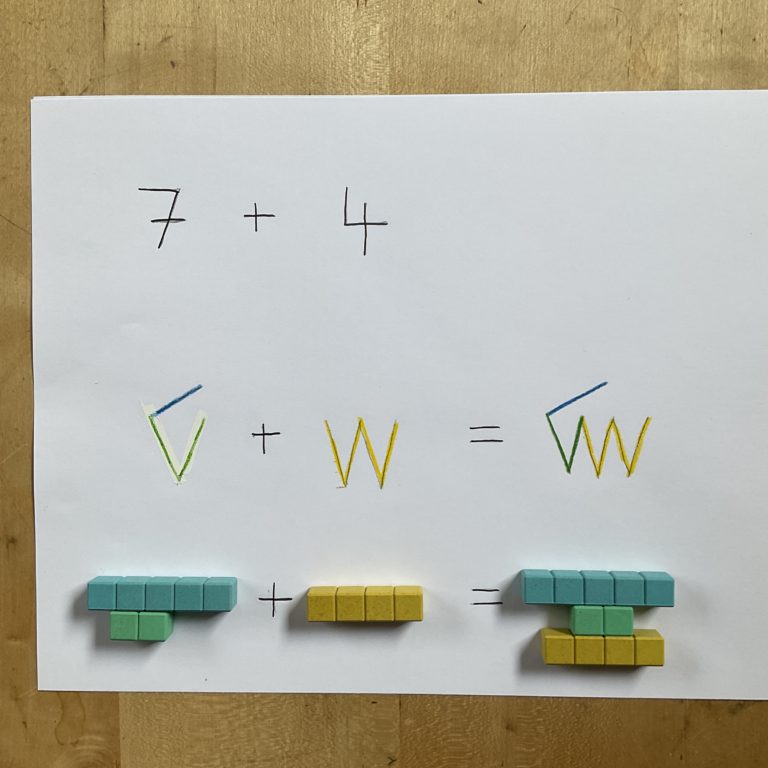
Der Übertrag entsteht dadurch, dass ich mehr als vier Einer habe, denn sobald ich fünf Einer habe, werden diese zu einem Fünfer umgewandelt. Ich streiche in meiner symbolischen Darstellung die fünf Einer einfach durch (nächstes Bild) und schreibe im nächsten Rechenschritt die neue Zahldarstellung hin – die Einer sind verschwunden und ein neuer blauer Fünferquerstrich ist aufgetaucht. Das entspricht dem Umtauschen der Zweierstange (grün) und der Viererstange (in gelb) in eine neue Fünferstange (blau). Außerdem habe ich einen roten Einer übrig:

Ich bin fertig:Das Ergebnis besteht aus zwei Fünfern und der Eins, also ist mein Ergebnis 11.
Addition mit Übertrag - ein bisschen komplizierter!
Hier habe ich noch ein Beispiel mit zweistelligen Zahlen im Kaktoviksystem und zwei Überträgen. Einmal werden Einer in Fünfer umgewandelt und dann nochmal die Fünfer in einen neuen Zwanziger. Zur Erinnerung: das Kaktoviksystem ist ein Zwanzigersystem, deswegen sind die Stellenwerte Potenzen der 20. Wenn die Zahlen einen höheren Wert als 19 haben, brauchen wir eine weitere Stelle, die genau wie in unserem Zehnersystem links neben die Einerstelle geschrieben wird. Hier ist die Aufgabe:
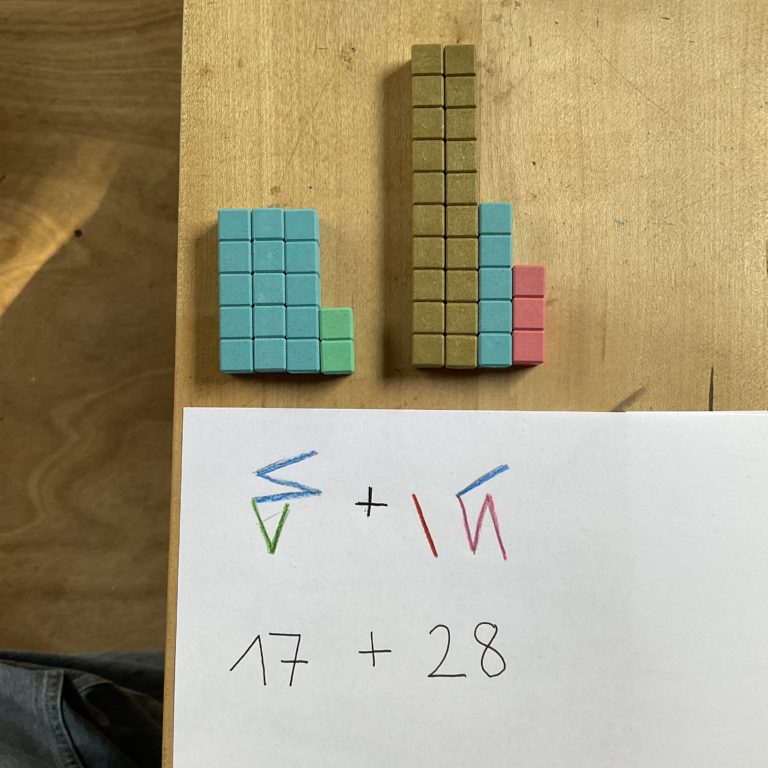
In die 28 passt genau 1 x 20 hinein – deswegen ist die vordere Stelle der zweiten Zahl eine Eins in rot. Dazu gehören die beiden goldenen Zehnerstangen obendrüber. Addieren bedeutet jetzt wieder „zusammenkippen“, deswegen schiebe ich die Materialien einfach zusammen und schreibe mir auch alle Striche in einer Zahl auf:
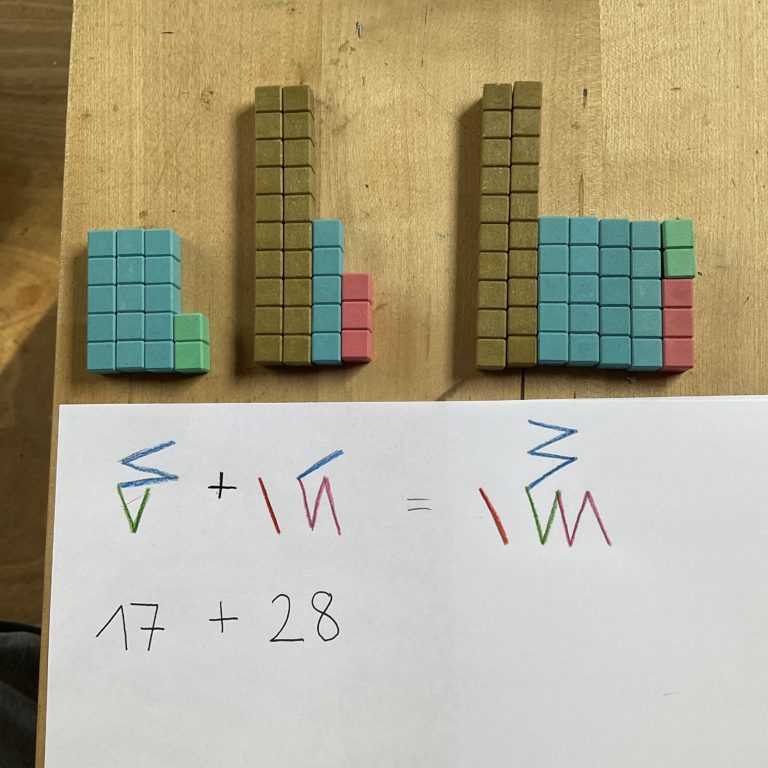
Nun kann ich mich um die Überträge kümmern.. Ich fange am besten bei den Einern an:
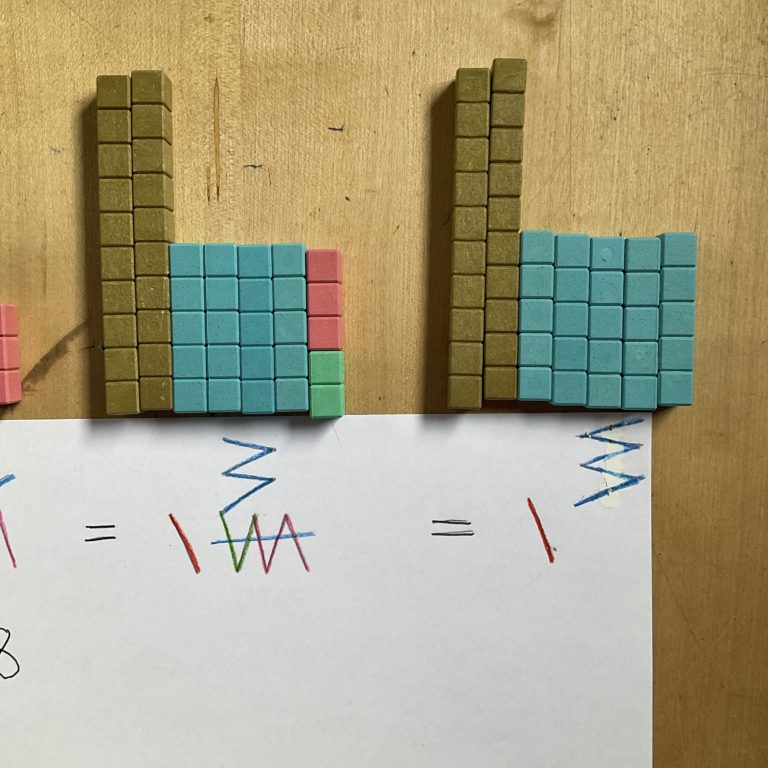
Die Schreibweise ist total praktisch: Ich streiche mir die fünf Einer durch und weiß, dass statt des ganzen Pakets ein Querstrich, also ein Fünfer oben dazukommt. Weil ich nun 5 Fünfer habe, streiche ich 4 Fünfer durch und ersetze sie im nächsten Schritt durch einen neuen Zwanziger, denn 4 x 5 ist 20. Der Übertrag von der Eins zur Fünf findet also bei 5 Einern statt, wohingegen der Übertrag von den Fünfern zur Zwnzig bei 4 Fünfern passiert:
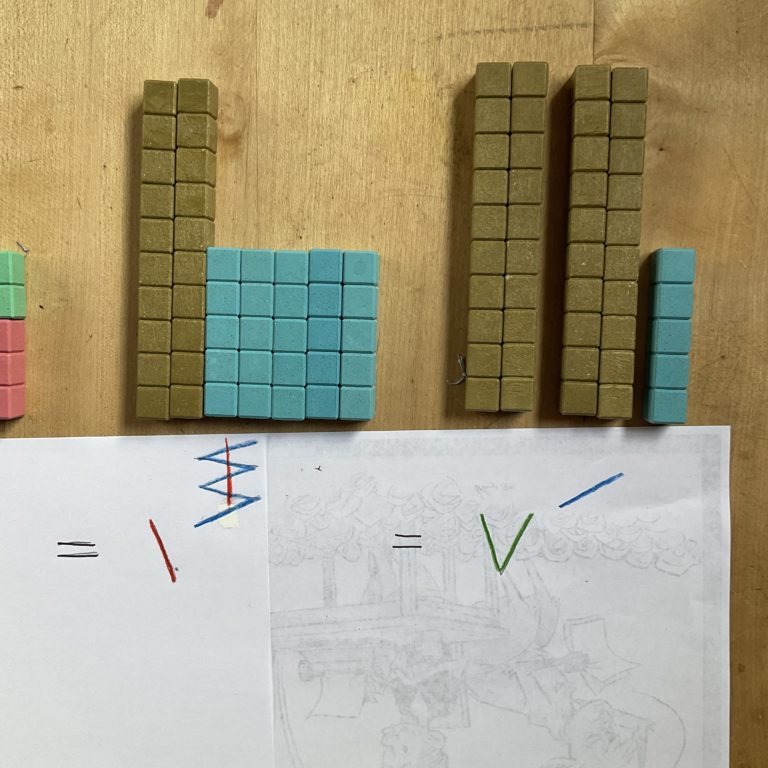
Jetzt bin ich fertig. Das Ergebnis ist 45, denn ich habe 2 x 20 und 1 x 5:
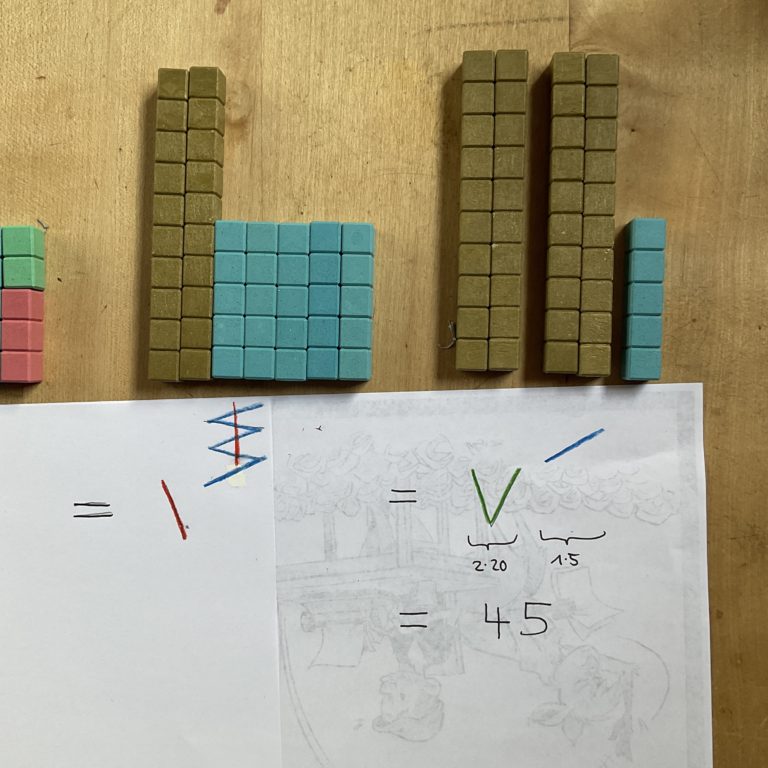
Wenn du bis hierhin durchgehalten hast, Gratulation! Ich hoffe, dir macht das Katkovik Zahlensystem soviel Freude wie mir! Es folgt noch ein Teil zur Multiplikation!